Здесь последовательно изложены все шаги урока в Stepic.
 Галилео Галилея часто называют основопололожником экспериментальной физики. Только эксприментально он смог опровергнуть умозрительную теорию Аристотеля о падении тел. Из метафизики Аристотеля следовало, что тяжелые тела должы падать быстрее легких.
Галилео Галилея часто называют основопололожником экспериментальной физики. Только эксприментально он смог опровергнуть умозрительную теорию Аристотеля о падении тел. Из метафизики Аристотеля следовало, что тяжелые тела должы падать быстрее легких.
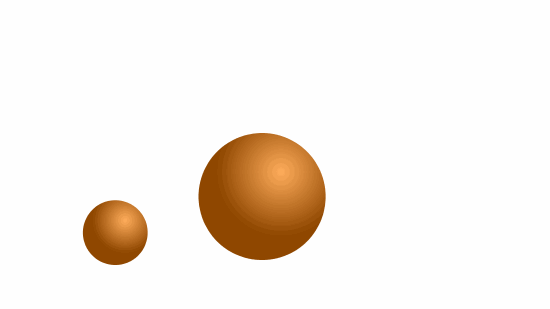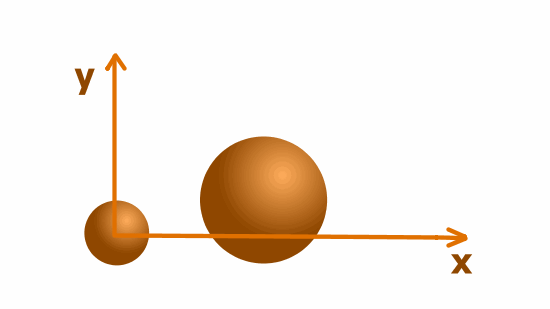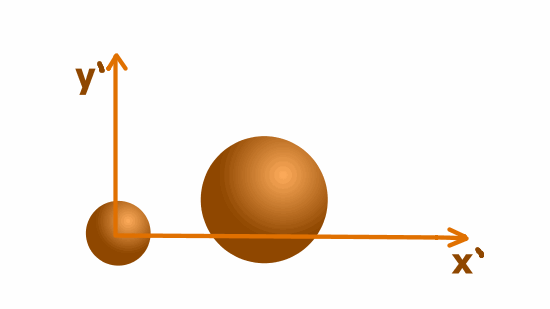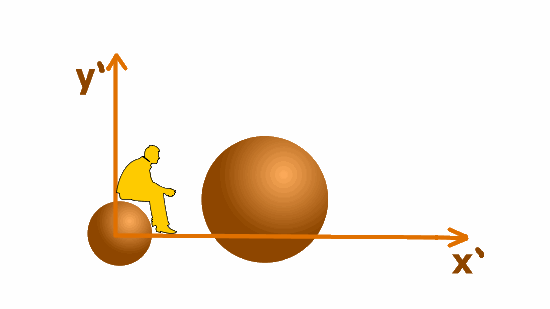
 Это уже опыт Animatron.
Это уже опыт Animatron.
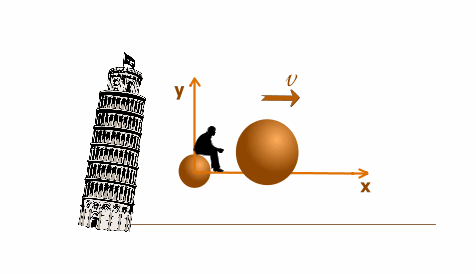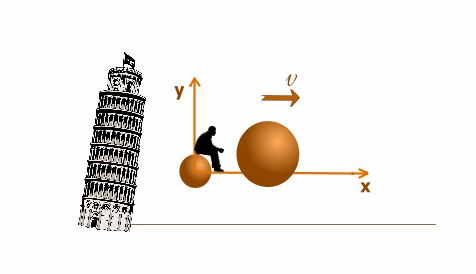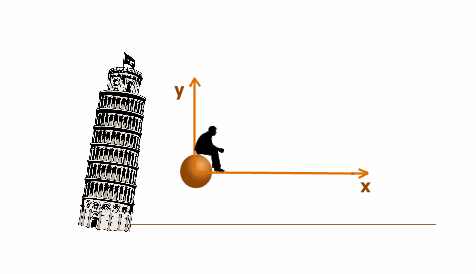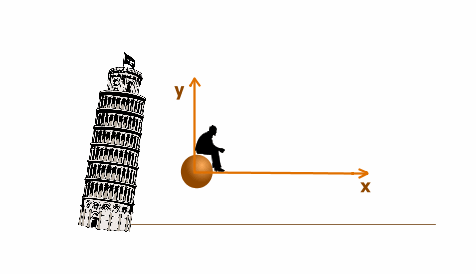
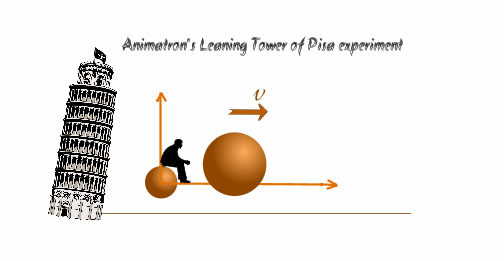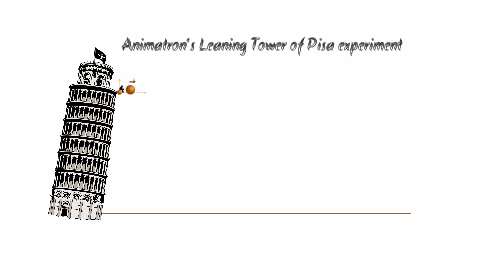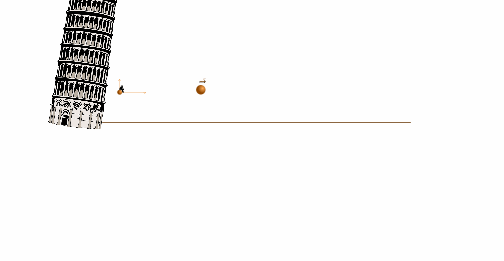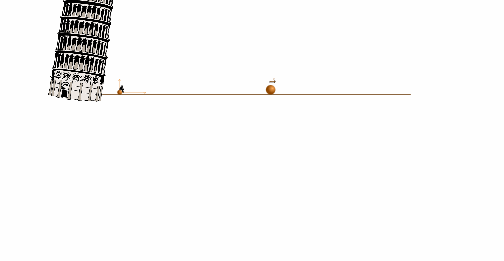
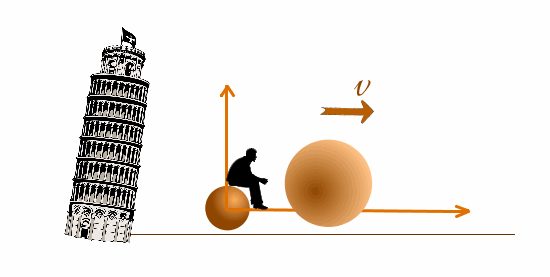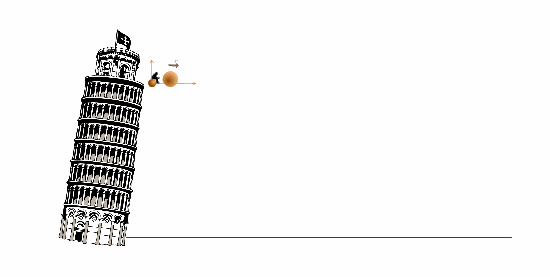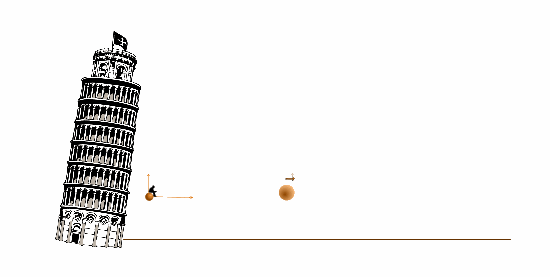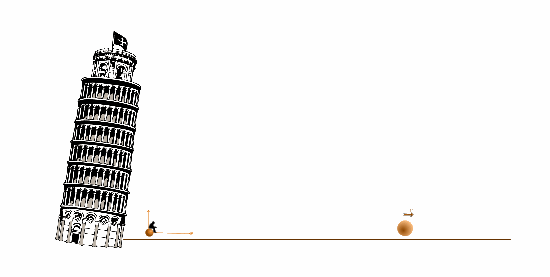
Мы поднимаем наблюдателя с двумя шарами и исследуем движение относительно системы отсчета х`y`, падающей с ускорениемg .
 Усложним задачу.
Усложним задачу.
 В падающей системе отсчета большой шар движется горизонтально, его траектория - прямая.
В падающей системе отсчета большой шар движется горизонтально, его траектория - прямая.
В системе отсчета, неподвижной относительно земли, тректория маленького шара - прямая, а большой шар движется по криволинейной траектории - параболе.

Напомню условие задачи.

Вторая попытка.
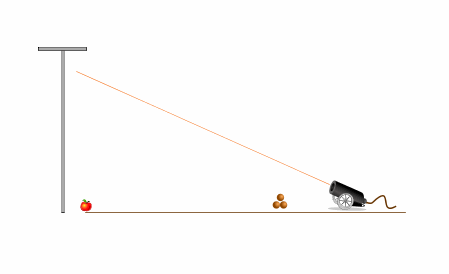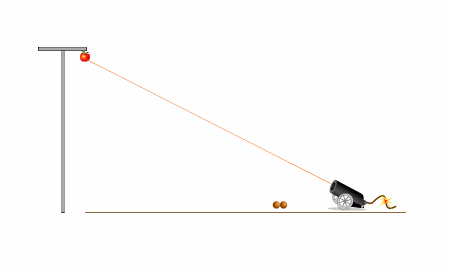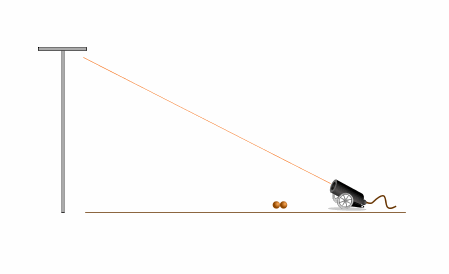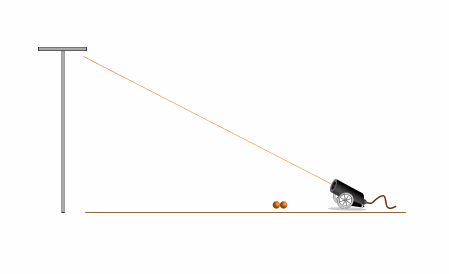 На левом рисунке - опыт в системе отсчета, связанной с землей. Яблоко падает ускоренно вниз. Ядро движется параболе, все больше и больше отклоняясь вниз от линии прицеливания.
На левом рисунке - опыт в системе отсчета, связанной с землей. Яблоко падает ускоренно вниз. Ядро движется параболе, все больше и больше отклоняясь вниз от линии прицеливания.
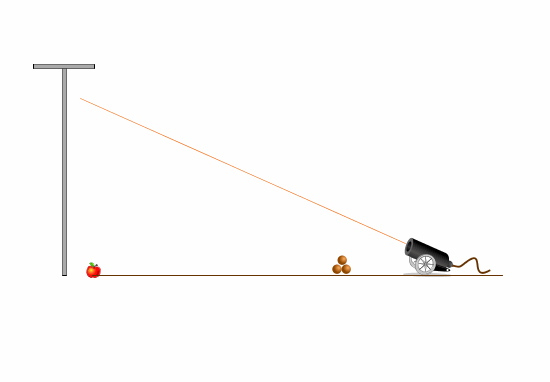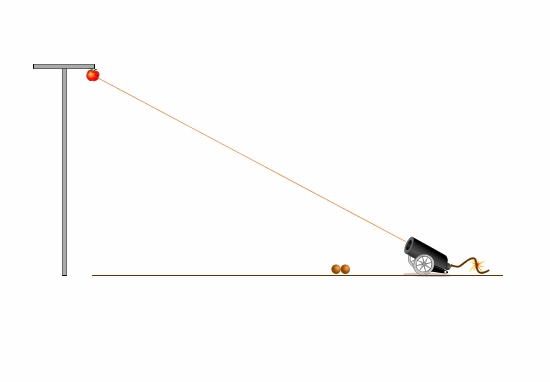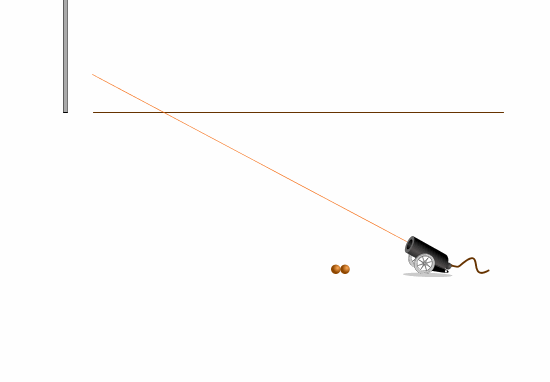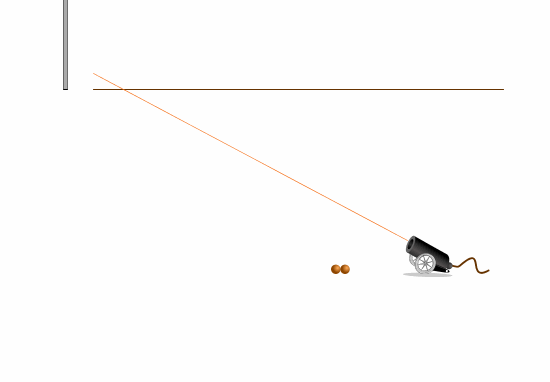
Задача формулируется так: как надо выстрелить в яблоко, которое начинает падать в момент выстрела, чтобы попасть в него?
Анализ будем проводить без формул. Использовать будем только возможности Аниматрон.
Галилей сформулировал принцип относительности движения для инерциальных систем отсчета. Но в кинематике равноправными являются любые системы отсчета, в том числе и движущиеся с ускорением относительно инерциальных.
Пользуясь экспериментально доказанным утверждением о том, что под действием силы тяжести за одно и то же время все тела смещаются на одинаковое расстояние вниз будем исследовать свободное падение тел в системе отсчета, падающей с ускорением g .
Если начальная скорость тела отлична от нуля, то в такой падающей системе отсчета эта скорость будет постоянна по направлению и величине, Состояние тел в такой системе отсчета можно назвать невесомостью.
В этом уроке рассмотрены методы изучения движения в разных системах отсчета, движущихся поступательно.
Согласно легенде, Галилей сбрасывая легку мушкетную пулю и тяжелоя пушечное ядро (200 грамм и 80 килограмм, соответственно) экспериментально доказал, что тела касаются земли одновременно.
Свой принцип относительности Галилей сформулировал для инерциальных систем отсчета. Однако для кинематики, гда рассмотривается только движение тел, и не рассматриваются причины, вызывающие это движение, все системы отсчета эквивалентны.
Под системой отсчета будем понимать систему координат x`y`, неподвижную относительно тела отсчета. Время будем считать текущим одинаково во всех рассматриваемых системах отсчета.
Команда Animatron проведет ряд экспериментов с использованием Пизанской башни. Наша цель - показать простой способ исследования движения тел в поле сил тяжести с использованием инструментария Animatron. Все рассуждения и объяснения - без формул.
Как доказал Галилей, все тела, падающие с одинаковой высоты и имеющие в начальный момент времени нулевые скорости касаются поверхности земли одновременно.
Выберем с качестве тела отсчета мушкетную пулю. Свяжем с ней систему отсчета x`y`.
Посадим для наглядности на мушкетную пулю наблюдателя. Относительно наблюдателя оба шара и система отсчета будут неподвижны во врмея падения..
Мы поднимаем наблюдателя с двумя шарами и исследуем движение относительно системы отсчета х`y`, падающей с ускорением
Как и следовало ожидать, шары неподвижны в этой системе отсчета. Обратите внимание, что на вашем экране шары тоже неподвижны во время падения Только Пизанская башня пролетает мимо наблюдателя и стремительно приблиается к нему земля.
Сообщим ядру начальную скорость, направленную вдоль оси 0x`.
и повторим наш эксперимент.
И система отсчета вместе с набюдателем и шары во время падения находятся на одном уровне на вашем экране.
В системе отсчета, неподвижной относительно земли, тректория маленького шара - прямая, а большой шар движется по криволинейной траектории - параболе.
Напомню условие задачи.
Стрельбы ведется из пушки по высоко висящему яблоку. Яблоко в момент выстрела начинает падать.
Надо так прицелиться, чтобы попасть в яблоко во время полета.
Первая попытка - стрелять ниже цели ("под яблочко") не оправдывает ожиданий.
Мимо.
Снаряд пролетел ниже цели.
Вторая попытка.
Пробуем прицелиться выше яблока.
Ядро во время полета под действием силы тяжести сильно отклоняется от линии прицела. Может, сейчас получится.
Вновь попытка оказывается безуспешной.
На правом рисунке показан тот же опыт в падающей вместе с яблоком системе отсчета. Хорошо видно, что траектория яблока - прямая. А яблоко так и вовсе неподвижно.
Комментариев нет:
Отправить комментарий